跳跃表是一种有序链表,通过维持多个指针指向不同结点用来进行快速访问,它支持平均O(logN),最坏O(N)的时间复杂度,在Redis中它是实现有序集合ZSET的底层实现之一。
1. 定义
Redis中,跳跃表实现如下图
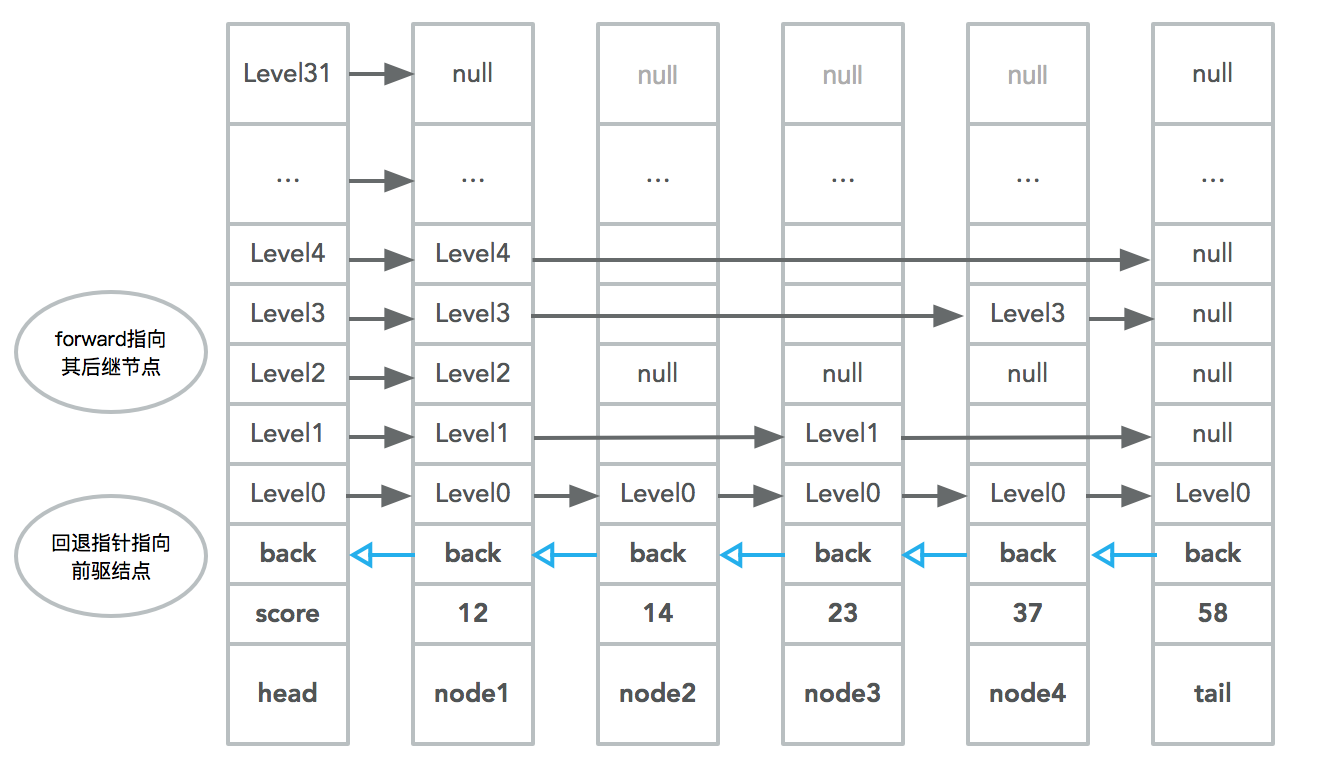
这个跳跃表的实现和 William Pugh的《Skip Lists: A Probabilistic Alternative to Balanced Trees》 中描述的基本相同,在下面3个方面做了修改:
a) 允许重复的分数
b) 比较的时候要考虑score和ele本身
c) 每个结点有一个回退指针,方便从尾部向头部遍历
1.1 跳跃表结点
ele 结点key,使用sds字符串存储,该值必须唯一。在字典中也有该ele结点(用于ZSETs使用)
score 存储结点分数值,可重复(此时通过ele排序),一般用来作为排序的参考,但有特殊情况会使用ele排序
backward 回退指针,当前结点的前驱结点,在从尾部遍历时非常方便
level
跳跃表实现的关键,每个元素包含多个level,每个level都可以指向其后方不同的结点,在搜索结点时通过自顶向下的方式搜索,可以大大节约搜索时间。
每次插入新结点时,通过幂次定律计算其要插入的level,以保证越高level的结点数量越少。
- forward 当前level指向的后继结点
- span 当前level后继结点与该结点所跨域结点的数量,计算排序时相当有用
1 | typedef struct zskiplistNode { |
1.2 跳跃表
1 | typedef struct zskiplist { |
2. 幂次定律
Redis中,使用返回随机level,该随机算法使用幂次定律。
1 | /** |
跳跃表的作用是为了替换平衡二叉树,跳跃表结构清晰简单、易于实现,利用随机化的性质让越高level的结点越少,其效率是极高的,平衡二叉树的维持平衡则需要进行大量的操作。
3. 源码剖析
跳跃表利用较小的空间代价,仅一些指针,提高了查找的效率。
查找结点的rank
从最高层开始遍历结点的level,通过先右后下的方式查找对应的结点
1 | /** |
- 创建一个新的跳跃表
1 | zskiplist *zslCreate(void) { |
跳跃表中插入结点
找到要插入结点的位置,并且记录所用需要修改level指针的结点
1 | zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) { |
- 删除结点
1 | /** |